CSAPP-DataLab

DataLab

Datalab的任务是实现一系列的位操作和算术运算函数，包括逻辑与、逻辑或、逻辑非、异或、加法、减法等。在给定的代码框架中填充空白部分，使得函数能够正确地执行对应的操作。

以下几个主要的内容：

1. 数据表示：了解不同数据类型的二进制表示方式，包括无符号整数、补码表示等，并熟悉各种数据类型之间的转换规则。
2. 位操作：使用位操作运算符（如与、或、非、异或等）来实现特定功能。这需要对位运算的原理和规则有一定的了解。
3. 算术运算：实现一些基本的算术运算函数，如加法、减法等。这可能涉及到溢出检测、符号位处理等问题。

bitXor

int bitXor(int x, int y) {
  return ~(~x&~y)&~(x&y);
}

 

copyLSB

先将x变成11111110或11111111，再加1

int copyLSB(int x){
	return ~(x&1)+1;
}

isEqual

返回值是0或1，可以异或后逻辑取反。

int isEqual(int x,int y){
	return !(x^y);
}

bitMask

通过全1的数位移可实现。

int bitMask(int highbit,int lowbit){
	int x = ~0;
	int a = x<<lowbit;
	int b = x<<highbit<<1;
	return (a^b)&a;
}

bitCount

int bitCount(int x) {
  int mask_1 = 0x55 << 8 | 0x55;
  int mask_2 = 0x33 << 8 | 0x33;
  int mask_4 = 0x0f << 8 | 0x0f;
  int mask_8 = 0xff << 16 | 0xff;
  int mask_16 = ~0 + (1 << 16);
  mask_1 |= mask_1 << 16;
  mask_2 |= mask_2 | mask_2 << 16;
  mask_4 |= mask_4 | mask_4 << 16;
  x = (x&mask_1) + ((x>>1)&mask_1);
  x = (x&mask_2) + ((x>>2)&mask_2);
  x = (x&mask_4) + ((x>>4)&mask_4);
  x = (x&mask_8) + ((x>>8)&mask_8);
  x = (x&mask_16) + ((x>>16)&mask_16);
  return x;
}

tmax

得到01111111

int tmax(void){
	return ~(1<<31);
}

isNonNegetive

根据符号位判断。

int isNonNegative(int x){
	return !(x>>31);
}

addOK

根据三个数的符号进行判断。

int addOK(int x,int y){
	int t = x + y;
	int sx = x>>31;
	int sy = y>>31;
	int st = t>>31;
	return !((~(sx^sy))&(sx^st));
}

rempwr2

取模操作的实现：对于x<0来说：先用a算出除数的相反数，再用b表示除数+余数，最后返回除数的相反数+除数+余数即可。对于x>=0来说：先用a算出除数的相反数，b为x除以2^n的余数，最后返回b即可。

int rempwr2(int x,int n){
	int a = (~0)<<n;
	int b = x&(~a);
	return b + (((x&(~b+1))>>0x1f)&a);
}

isLess

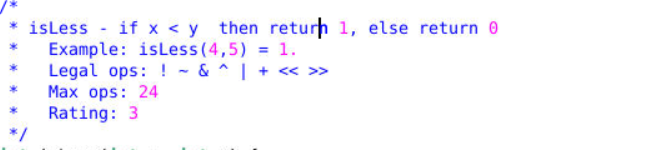
x<y一般会有三种情况
x < 0 ,y<0 x-y>0
x>0, y>0 x-y<0 ;
x<0 ,y>0

因为会有减法出现，先将y取反
z = ~y ;

可以得到一个显而易见的结果：
x = z =1的时候，(x&z) 得最高位= 1 ；
或者x!=z的时候，(x+z+1) ^ x得最高位为1；

则表达式为
return (((x+z+1)&(x^z)|(x&z))>>31)&0x1;

int isLess(int x,int y){
	int ny = ~y;
	return ((((x+ny+1)&(x^ny))|(x&ny))>>0x1f)&1;
}

absVal

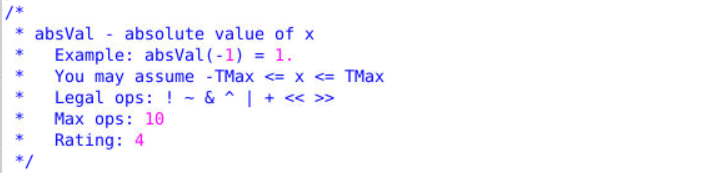
负数和正数的区别在与最高位的1/0，可使用^1或^0，来得到负数的取反操作且正数保持不变。取反已完成，还剩下一个＋1操作。此+1操作要使负数才+1而正数是+0。利用它们的区别，负数最高为1，正数最高为0.1+1=0+1=1，0+1。我们可以使用溢出来完成。即((x>>31)+1)。当负数时(0xffffffff)+1=1,当正数~(0x00000000)+1=0(溢出)。

int absVal(int x){
	int y = x>>31;
	return (y&(~x+1))+((~y)&x);
}

isPower2

每个数在二进制中都是唯一的。也就是2的幂，在二进制中只有一位是1其他全是0才有可能是2的幂(除了第一位是1不是2的幂)即可以用x&(x-1)来判断，如果只有一个1返回0，加个!，!(x&(x+(0)))。还要判断是不是负数，是负数就返回0(!!(x>>31)还要判断是不是0，是0也要返回0!!x

int isPower2(int x){
	return ((!(x&(x+~0)))&((~(x>>31)&(!!x))));
}

float_neg

函数要求：

返回浮点参数f的表达式-f的位等效项。参数和结果都作为无符号int传递，但是它们将被解释为单精度浮点值的位级表示。 当参数为NaN时，返回参数。

函数的参数可能为NaN，所以需要进行判断。如果参数uf的第23位到第30位全为1，而且uf的低23位不为0，这说明uf解释为单精度浮点值的位级表示时是一个NaN，所以应该直接返回，否则应直接将uf的最高位（符号位）取反即可得到-f。

unsigned float_neg(unsigned uf){
	unsigned w,x,y,z,t;
	w = (1<<23)-1;
	x = 0xff<<23;
	y = uf&w;
	z = uf&x;
	if((z==x)&&y){
		return uf;
	}
	return (1<<31)^uf;
}

float_half

函数要求：

函数实现：

float_i2f

函数实现：